05. Graph Practice

Question:

Let's discuss a few more definitions that extend on the topics from the last few videos.

Talking about connectivity in a directed graph is a bit more complicated than in an undirected graph. Let's look at some more definitions:

Disconnected

Disconnected graphs are very similar whether the graph's directed or undirected—there is some vertex or group of vertices that have no connection with the rest of the graph.

Weakly Connected

A directed graph is weakly connected when only replacing all of the directed edges with undirected edges can cause it to be connected. Imagine that your graph has several vertices with one outbound edge, meaning an edge that points from it to some other vertex in the graph. There's no way to reach all of those vertices from any other vertex in the graph, but if those edges were changed to be undirected all vertices would be easily accessible.

Connected

Here we only use "connected graph" to refer to undirected graphs. In a connected graph, there is some path between one vertex and every other vertex.

Strongly Connected

Strongly connected directed graphs must have a path from every node and every other node. So, there must be a path from A to B AND B to A.

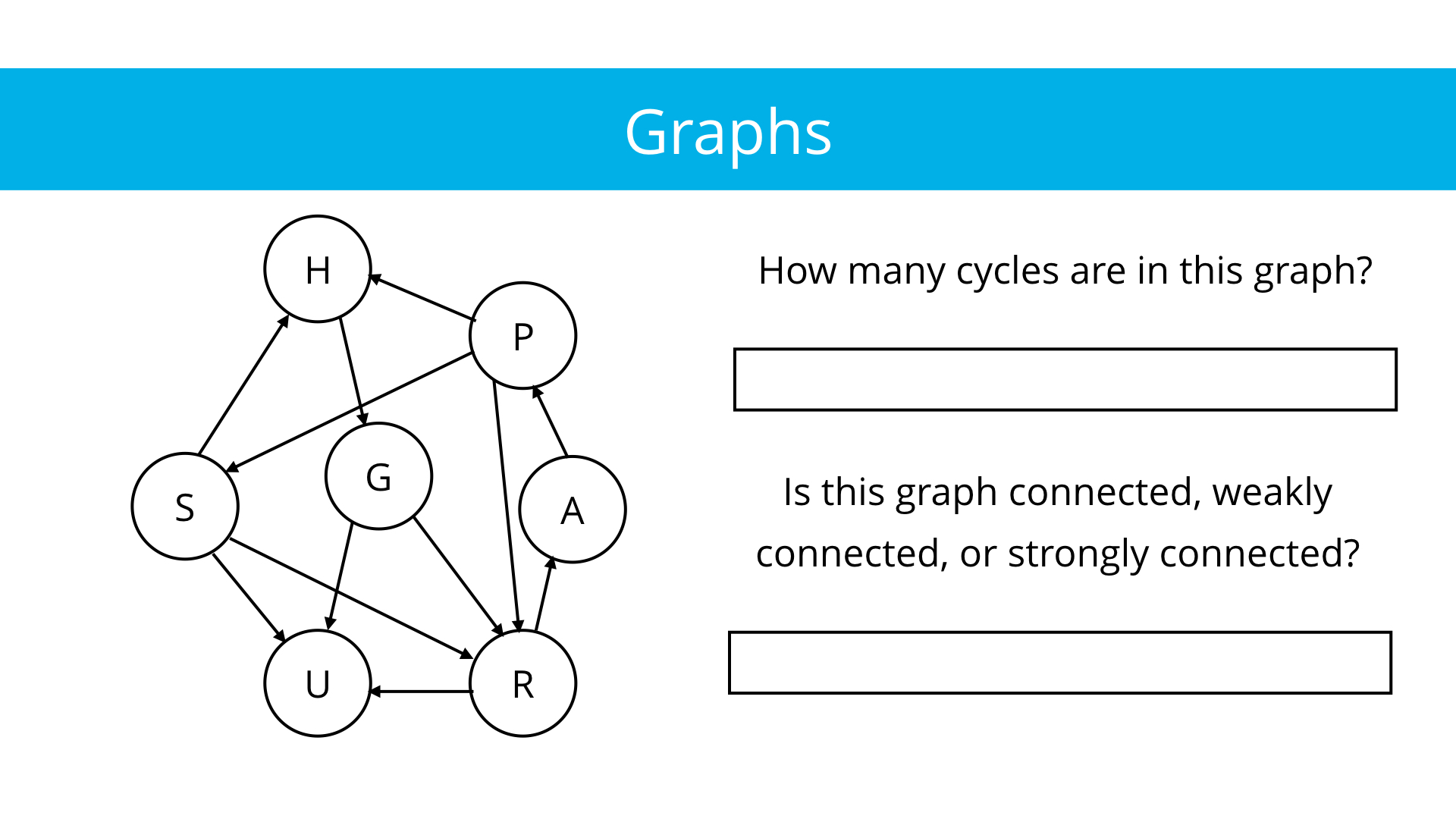
Solution:

Let's take a look at that image again:

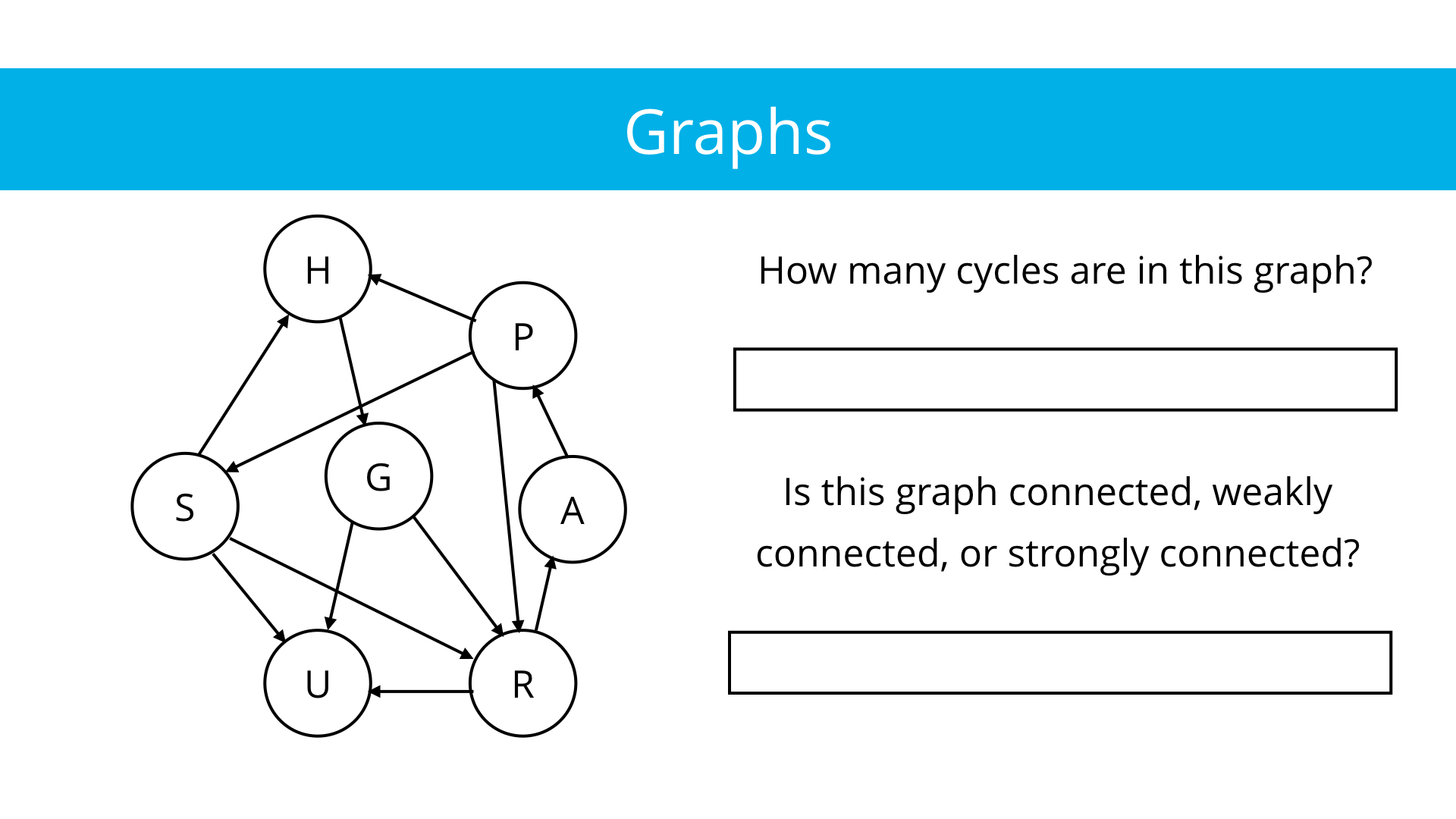
First, let's count the cycles:

• G->R->A->P->H->G
• R->A->P->R
• R->A->P->S->R

Now, let's talk connectivity. There's one vertex, U, that has only inbound edges—meaning only edges that point to it. Thus, the graph can't be strongly connected. Even if every vertex has a path to U, it doesn't have a path to any of them.

However, if you converted every edge to an undirected edge, it would be connected. Therefore we can label this graph "weakly connected".